Descriptive Statistics
- Upendra Kumar
- Jul 26, 2021
- 6 min read
Updated: Aug 18, 2021
Population: Group from which a sample is drawn. The exact population will depend on the scope of the study.
Sample: A sample is a small group of members selected from a population to represent the population. A subset of the population is called a sample.

Sampling: Sampling is a method that allows researchers to infer information about a population based on results from the sample.
Broadly Sampling is divided into two categories:
Probability Sampling: Probability sampling is based on the fact that every member of a population has a known and equal chance of being selected.
Non Probability Sampling: It involves non-random selection based on convivence.
Probability Sampling:
Simple Random Sampling: A probability sample in which every member of a study population has an equal chance of selection.
Systematic Sampling: The first element is selected randomly from a list or from sequential files, and then every nth element is selected. Suppose after taking a random sample, we choose every 10th element from the population.
Cluster Sampling: A probability sampling procedure that involves randomly selecting clusters of elements from a population and subsequently selecting every element in each selected cluster for inclusion in the sample. For example, in this sampling technique, we divide the population into various clusters let say 4 clusters, and then from each cluster, we select elements subsequently.
Stratified Sampling: A probability sampling procedure that involves dividing the population into groups or strata defined by the presence of certain characteristics (e.g., race, gender, location, etc. )and then random sampling from each stratum.
Non Probability Sampling:
Convenience Sampling: This sampling technique involves selecting samples based on convenience. Also known as Accidental Sampling.
Snowball Sampling: Select samples and ask them to refer you to others. Also known as Network Sampling.
Quota Sampling: Quota sampling means to take a very tailored sample that's in proportion to some characteristic or trait of a population. For example, let's select males from a population of age above 50.
Purposive/ Judgmental Sampling: Selecting samples based on his or her own judgment.
What is Data in statistics?
Data are individual pieces of factual information recorded and used for the purpose of analysis. It is the raw information from which statistics are created. Statistics are the results of data analysis, interpretation, and presentation.
We can divide data based on their types and on their measurement levels.
Data based on their types:
Categorical data: Categorical data represent types of data that may be divided into groups. Examples of categorical data are race, sex, age group, car brand, etc.
Numerical data: Numerical data is a data type expressed in numbers, rather than natural language description. It is always collected in number form. It is further divided into discrete and continuous data.
Before we go on discrete and continuous data, we need to know what is a Random variable.
A random variable, usually written X, is a variable whose possible values are outcomes of a random phenomenon or experiment. There are two types of random variables, discrete and continuous.
Discrete random variable: A discrete random variable has a countable number of possible values.
For example the number of students in a class, the number of phones you can have, the number of children in a family-like 0,1,2,3.
Continuous random variable: A continuous random variable is one that takes an infinite number of possible values. For example between 1 and 2, we can find an infinite number of values. Continuous random variables are usually measurements. For example weight of a man, height of a man.
Data based on their Measurement levels:
Based on measurement levels data is further divided into:
Qualitative data
Quantitative data
Qualitative data is further divided into:
Nominal Scale
Ordinal Scale
Quantitative data is further divided into:
Interval Scale
Ratio Scale
One by one we will put light on each of these topics. Let's start by describing Nominal Qualitative data.
Nominal Scale: It is simply a system of assigning numbers/symbols to events in order to label them. Like: assignment of numbers to cricket players in order to identify them. This is just a way of keeping track of people, objects, and events. One cannot do much with the numbers involved.
It is the least powerful level of measurement. It indicates no order or relationship and has no arithmetic origin. It simply describes the difference between things by assigning them numbers.
Ordinal Scale: It places events in order, but doesn't make the intervals of the scale equal. Like: Sam's position in his class is 10th and Mark's position is 20th. Then it can't be said that Sam's position is twice as good as that of Mark.
Ordinal Scales only permit the ranking of items from highest to lowest or lowest to highest and have no absolute values and the real differences between adjacent ranks may not be equal. Since the numbers of this scale have only a rank meaning, the appropriate measure of central tendency is Median.[If you don't know what is a central tendency is, don't worry in the next section we are going to cover that part]
Interval Scale: In this type of scale, the interval is adjusted in terms of some rules that have been established as a basis for making the units equal. Interval scales provide more powerful measurements than Ordinal scales because the Interval scale also incorporates the concept of equality of interval.
Marks Number of Students
Less than 10 2
10-20 4
20-30 8
30-40 10
Mean is the most appropriate measure of central tendency, while standard deviation is the most widely used measure of dispersion.
Ratio Scale: The ratio scale represents the actual amount of variables, which also includes absolute or true zero of measurement. It is mainly used for measuring physical dimensions such s Height, Weight, Distance, etc. Like: the zero point on centimeter-scale indicate the complete absence of height or length.
with ratio scales, one can make statements like: "John's typing performance was twice as good as that of Robert's." Generally, all statistical techniques are useable with ratio scales and all calculations that one can carry out with real numbers can also be carried out with ratio scale values.

The measure of Central Tendency:
A measure of central tendency provides a very convenient way of describing a set of scores with a single number that describes the performance of the group.
We have three different measures of central tendency:
Mean: It is the arithmetic average of the set of values. It is the measure of the center of data. To calculate the mean we need to simply divide the sum of all the values of a set by the total number of values.
For example: Let suppose we have 10 students in a class and we want to calculate their mean height. Then mean height = Sum of the height of all 10 students/10
In the field of statistics, we denote population means by a greek symbol (μ) and sample mean denoted by X bar.
X bar = x1 + x2 + x3 + x4 + ..............+ xn/n
Mean is sensitive to the outlier, If in the data set too many outliers are there, then the mean is going to be influenced by those outliers and not going to give accurate inference of the population mean.
Median: Median is the central value in the sense that there are as many values smaller than it as there are larger than it.
To calculate median, we first need to arrange values in ascending order and then:
If n is odd, then median = n + 1/2
If n is even, then median = (n/2 + n + 1/2)/2
The Median is not sensitive to outliers. We prefer to use the median as a measure of the central tendency when we have too many outliers present in our dataset.
Mode: Mode is the most frequently occurring value in a given set. We use mode mostly with the categorical variables. Suppose in a dataset we have a gender column and on that gender, column female has occurred most of the time. Then in that case mode for the gender column is going to be female.
The model can also be of many types such as:
Unimodal for one mode.
Bimodal for 2 modes.
Multimodal for more than 2 modes.
The measure of Dispersion
A measure of dispersion indicates the scattering of data. In other words, dispersion is the extent to which values in a distribution differ from the average of the distribution. It gives us an idea about the extent to which individual items vary from one another and the central value.
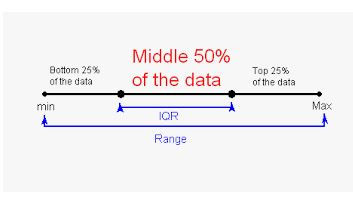
Range: In statistics, the range of a set of data is the difference between the largest and smallest values.
Let X is a set of data, then Range = X(max) - X(min)
X = 1,2,3,4,5,6,7,8,9
Range = X(max) - X(min) = 9 - 1=8
The range can give us a rough idea of how the outcome of the data set will be before we look at it actually. The difference here is specific, as it tells us to what extent we can have data points.
The range is the size of the smallest interval (statistics) which contains all the data and provides an indication of statistical dispersion.
It is measured in the same units as the data.
Since it only depends on two of the observations, it is most useful in representing the dispersion of small data sets.


Comments